TEORÍA DE JUEGOS
v1 = 4 + δ ≤ 10 v2 = 9 + ε ≤ 17 v3 = 6 + η ≤ 14
δ ≤ 6 ε ≤ 8 η ≤ 8 3 ≤ δ + ε 3 ≤ δ + η 7 ≤ δ + η 11 = δ + ε + η
Para 3:
Por tanto, el valor de Shapley para 3 es:
La solución de Shapley será:
Cualquier asignación que verifique lo siguiente será núcleo:
Ejemplo 1:
Supongamos que en cierto proceso electoral hay un aspecto referente a cual de dos ciudades (A o B) le sera construido un sistema de transporte masivo. Hay solo dos candidatos a la presidencia y cada uno de estos debe anunciar a cual de las dos ciudades se compromete a construirle el sistema de transporte, o evadir el tema en sus apariciones públicas. Cada candidato busca obtener el mayor porcentaje posible de los votos de las dos ciudades. Los votantes de las demás ciudades son indiferentes respecto al tema. Los porcentajes de votos que obtiene el candidato 1 dadas las elecciones de 1 y 2 aparecen en la matriz de la
gura 1. As, por ejemplo, si el candidato 1 se compromete a construirle el sistema de transporte masivo a la ciudad A, mientras el candidato 2 se compromete a construírselo a B, cada uno obtendrá a el 50% de los votos. Para encontrar el valor maxmin de este juego, inicialmente tomemos como dada la elección del candidato 1 y encontremos la estrategia de 2 que minimiza el pago de 1; as, independientemente de la elección del candidato 1, el candidato 2 decide evadir el tema, con lo que los pagos mínimos para el candidato 1 (porcentajes de votación ) son 40 %, 50% o 40 %; como este debe ahora maximizar su pago mínimo, elegira \construirle a B"y as, la repartición del electorado sera 50 %-50 %, con lo que el valor maxmin es, efectivamente, v1 = 0;5.
SOLUCIÓN:
Se tiene el siguiente cuadro:
Encontremos ahora el valor minmax; para las elecciones del candidato 2 "Construirle a A, Construirle a B" y "Evadir el tema", los máximos pagos para el candidato 1 son 60 %, 55% y 50 %, respectivamente. Como el candidato 2 debe minimizar estos pagos, elige "Evadir el tema", con lo que el valor minmax es v2 = 0;5. Observemos que, en este juego,
v1 = v2 = 0;5.
Ejemplo 2:
En una ciudad existen gran cantidad de academias y tres de ellas son las mejores:
1) A1: especialista en letras
2) A2: especialista en ciencias
3) A3: especialista en idiomas
Uno se apunta a asignaturas. Y además, si las materias estuvieran juntas, la gente se matricularía en más.
Datos que se dan:
1) Si se agrupan A1 y A2 tendrán 16.000 cursos o asignaturas
2) Si se agrupan A1 y A3 tendrán 13.000
3) Si se agrupan A2 y A3 tendrán 20.000
4) Si se agrupan A1, A2 y A3 tendrán 30.000
5) Si va sola A1 tendrán 4.000
6) Si va sola A2 tendrá 9.000
7) Si va sola A3 tendrá 6.000
Se pide:
1) Construir la función característica que define el juego.
2) Ver si se cumple o no la propiedad superaditiva
3) Calcular en núcleo
SOLUCIÓN:
Para solucionar este problema, tomaremos los datos en miles de pesetas.
1) La función característica es:
f(∅) = 0
f(A1) = 4 f(A2) = 9 f(A3) = 6
f(A1,A2) = 16 f(A1,A3) = 13 f(A2,A3) = 20
f(A1,A2,A3) = 30
2) Propiedad superaditiva. La cumple ya que:
a) f(A1,A2) = 16 > 4 + 9 = f(A1) + f(A2)
b) f(A1,A3) = 20 > 4 + 6 = f(A1) + f(A3)
c) f(A2,A3) = 20 > 9 + 6 = f(A2) + f(A3)
d) f(A1,A2,A3) = 30 > 16 + 9 = f(A1, A2) + f(A3)
e) f(A1,A2,A3) = 30 > 13 + 9 = f(A1,A3) + f(A2)
f) f(A1,A2,A3) 30 > 20 + 4 =f(A2,A3) + f(A1)
Hay interés real en unirse en coaliciones, ya que todas las anteriores desigualdades son estrictas.
3) Cualquier asignación será del núcleo si y solo si verifica:
4 ≤ v1 9 ≤ v2 6 ≤ v3
16 ≤ v1 + v2 13 ≤ v1 + v3 20 ≤ v2 + v3
v1 + v2 + v3 = 30
Más aún, como:
vi ≤ f(A1,A2,A3) - f({A1,A2,A3}-{i})
también debe verificarse:
v1 ≤ 30 - 20 = 10 v2 ≤ 30 - 13 = 17 v3 ≤ 30 - 16 = 14
luego las soluciones serán del tipo siguiente:
f(A1,A2,) + v3 ≤ f(A1,A2,A3)
Por tanto:
v3 ≤ f(A1,A2,A3) - f(A1,A2)
Si aplico la anterior expresión a (5), (6) y (7) tendré:
a) v1 ≤ 30 - 20 = 10
b) v2 ≤ 30 - 13 = 17
c) v3 ≤ 30 - 16 = 14
En definitiva, para que el reparto sea núcleo debe cumplir:
v1 = 4 + δ ≤ 10 v2 = 9 + ε ≤ 17 v3 = 6 + η ≤ 14
con :
δ ≤ 6 ε ≤ 8 η ≤ 8 3 ≤ δ + ε 3 ≤ δ + η 7 ≤ δ + η 11 = δ + ε + η
Ejemplo 3:
Hay tres municipios que precisan los servicios de una planta depuradora. Para cada
uno de los tres, presenta los siguientes costes:
1) C(1) = 50
2) C(2) = 30
3) C(3) = 10
Si hacen depuradoras conjuntas:
1) C(1, 2) = 65
2) C(1, 3) = 55
3) C(2, 3) = 35
4) C(1, 2, 3) = 75
La función de pagos o rendimientos de cada coalición la definimos, en este problema,
como los costes individuales menos lo que les cuesta en esa coalición. Es decir:
f(∅) = 0
f(1,2,3) = [C(1) + C(2) + C(3)] - C(1,2,3) = (50 + 30 + 10) - 75 = 15
f(1,2) = [C(1) + C(2)] - C(1,2) = (50 + 30) - 65 = 15
f(1,3) = [C(1) + C(3)] - C(1,3) = (50 + 10) - 55 = 5
f(2,3) = [C(2) + C(3)] - C(2,3) = (30 + 10) - 35 = 5
f(1) = C(1) - C(1) = 50 - 50 = 0
f(2) = C(2) C(2) = 30 - 30 = 0
f(3) = C(3) - C(3) = 10 - 10 = 0
Dicha función de pagos, se puede comprobar que cumple la propiedad superaditiva. Es
decir: f(S) + f(T) ≤ f(S∪T) con S ∩ T = ∅
Se pide:
1) Calcular el valor de Shapley
2) Calcular el núcleo
Solución:
Vamos a empezar calculando el valor de Shapley
Para 1:
Por tanto, el valor de Shapley para 1 es:
Para 2:
Por tanto, el valor de Shapley para 2 es:
Para 3:
Por tanto, el valor de Shapley para 3 es:
La solución de Shapley será:
Cualquier asignación que verifique lo siguiente será núcleo:
v1 + v2 + v3 = 15
0 ≤ v1
0 ≤ v2
0 ≤ v3
15 ≤ v1 + v2
5 ≤ v1 + v3
Como vi ≤ f(N) - f(N-{i}) tendré:
v1 ≤ 15 - 5 = 10
v2 ≤ 15 - 5 = 10
v3 ≤ 15 - 15 = 0
Por tanto, el núcleo cumplirá:
v1 + v2 = 15
5 ≤ v1 ≤ 10
5 ≤ v2 ≤ 10
v3 = 0
Obsérvese que la solución de Shapley no pertenece al núcleo.
Ejemplo 4:
Sean tres academias:
1) A1: especialista en letras
2) A2: especialista en ciencias
3) A3: especialista en idiomas
cuya función característica es:
f(∅) = 0
f(A1) = 4, f(A2) = 9, f(A3) = 6,
f(A1,A2) = 16, f(A1,A3) = 13, f(A2,A3) = 20,
f(A1,A2,A3) = 30.
Se pide calcular el valor de Shapley
Solución:
Para A1:
Por tanto, el valor de Shapley para A1 es:
Para A2:
Por tanto, el valor de Shapley para A2 es:
Para A3:
Por tanto, el valor de Shapley para A3 es:
La solución de Shapley será:
(VSA1+ VSA2+ VSA3) = (7, 13, 10)
La segunda academia era la que individualmente tenía más alumnos. Por lo tanto, es
lógico que en la solución de Shapley obtenga un valor mayor.
Ejemplo 5:
Dos bancos del sistema compiten por atraer el mayor número de cuenta
habientes en un poblado del occidente del país: Banco “Le cuido su pisto” el
primero, y Banco “ Le Guardo su Plata” el segundo; para el logro de su objetivo
cada uno aplica las estrategias siguientes:
1. Sorteo de electrodomésticos
2. Tasa de interés más alta
3. Sorteo de dinero en efectivo
1. Sorteo de electrodomésticos
2. Tasa de interés más alta
3. Sorteo de dinero en efectivo
Si el segundo banco ofrece sorteo de electrodomésticos
atrae 200 cuenta habientes más que el primero, cuando este ofrece lo mismo,
1000 más cuando el primero ofrece tasa de interés mas alta y 800 menos cuando
el primero ofrece sorteo de dinero en efectivo.
Si el segundo banco ofrece una tasa de interés más alta atrae 1300 más
cuando el primero ofrece sorteo de electrodomésticos, 700 más cuando el primero
ofrece lo mismo y 900 menos cuando el primero ofrece sorteo de dinero en
efectivo. Si el segundo banco ofrece sorteo
de dinero en efectivo atrae 2000 menos cuando el primero ofrece sorteo de
electrodomésticos, 1500 más cuando el primero ofrece tasa de interés más alta y
850 menos cuando el primero ofrece lo mismo.
1. ¿Que banco es el ganador del juego?
2. ¿Qué estrategia debe aplicar cada banco?
3. ¿En un año cuantos meses debe aplicar cada estrategia?
4. ¿Cuántos cuenta habientes atrae más el banco ganador?
5. Si el primer banco ofrece sorteo de dinero en efectivo y el segundo sorteo de
electrodomésticos, el segundo atrae 800 cuenta habientes más que el primero.
¿Cuales serán las nuevas respuestas?
1. ¿Que banco es el ganador del juego?
2. ¿Qué estrategia debe aplicar cada banco?
3. ¿En un año cuantos meses debe aplicar cada estrategia?
4. ¿Cuántos cuenta habientes atrae más el banco ganador?
5. Si el primer banco ofrece sorteo de dinero en efectivo y el segundo sorteo de
electrodomésticos, el segundo atrae 800 cuenta habientes más que el primero.
¿Cuales serán las nuevas respuestas?
Solución:
R = BCO. “LE CUIDO SU PISTO”
C =
BCO. “LE CUIDO SU PLATA”
Estrategias:
X1 ,Y1
– sorteo de electrodomésticos
X2 ,Y2 – tasa de interés más alta
X3 ,Y3 – sorteo de dinero
en efectivo
Construir matriz de juego:
C
|
CF
|
||||||
Y1
|
Y2
|
Y3
|
< FILA
|
||||
X1
|
-200
|
-1300
|
2000
|
-1300
|
MAXMIN = 800
|
||
R
|
X2
|
-1000
|
-700
|
-1500
|
-1500
|
||
X3
|
800
|
900
|
850
|
800
|
|||
> COLUMNA
|
800
|
900
|
2000
|
MINMAX = 80
MAXMIN = MINMAX PUNTO DE SILLA = 800
800 = 800 VALOR DE JUEGO = 800
MAXMIN = MINMAX PUNTO DE SILLA = 800
800 = 800 VALOR DE JUEGO = 800
RESPUESTAS:
1. Favorece al Bco. “Le cuido su pisto”.
2. R = Utiliza estrategias X3 = sorteo dinero en efectivo
C= Utiliza estrategias Y1 = sorteo de electrodomésticos
3. R = 12 meses
C = 12 meses
4. 800 Clientes
5. R => X3
1. Favorece al Bco. “Le cuido su pisto”.
2. R = Utiliza estrategias X3 = sorteo dinero en efectivo
C= Utiliza estrategias Y1 = sorteo de electrodomésticos
3. R = 12 meses
C = 12 meses
4. 800 Clientes
5. R => X3
C =>
Y1
C
|
CF
|
||||||
Y1
|
Y2
|
Y3
|
< FILA
|
||||
X1
|
-200
|
-1300
|
2000
|
-1300
|
MAXMIN = - 800
|
||
R
|
X2
|
-1000
|
-700
|
-1500
|
-1500
|
||
X3
|
800
|
900
|
850
|
800
|
|||
> COLUMNA
|
800
|
900
|
2000
|
MINMAX = 800
MAXMIN = MINMAX PUNTO DE SILLA = no hay
-800 = -200 VALOR DE JUEGO = si hay SIMPLEX
SIMPLEX
En función: “Y” (Maximización)
F.O.Max = Y1 + Y2 + Y3
Sujeto a: (Restricciones)
1.
–200Y1
+ (-1300) Y 2 + 2000 Y 3
£
1 Ü siempre será 1
porque la probabilidad no
2.
–1000Y1
- 700 Y 2 - 1500 Y 3 £
1 puede ser mayor a 1
3.
-800 Y1
+ 900 Y2 + 850 Y
3 £ 1
4.
Y1;
Y2 & Y3 ³ 0
Convertir en ecuaciones agregando variables de holgura:
5.
–200Y1
+ (-1300) Y 2 + 2000 Y 3 =
1 Ü siempre será 1
porque la probabilidad no
6.
–1000Y1
- 700 Y 2 -
1500 Y 3 =
1 puede ser mayor a 1
7.
-800 Y1
+ 900 Y2 + 850 Y
3 = 1
8.
Y1; Y2 & Y3
³ 0
Y1
|
Y2
|
Y3
|
Y4
|
Y5
|
Y6
|
C
|
-200
|
-1300
|
2000
|
1
|
0
|
0
|
1
|
-1000
|
-700
|
-1500
|
0
|
1
|
0
|
1
|
-800
|
900
|
850
|
0
|
0
|
1
|
1
|
-1
|
-1
|
-1
|
En función: “X” (Minimización)
F.O. Min z = X1 + X2
+X3
Sujeto a:
1.
–200Y1 + (-1300) Y 2 + 2000 Y 3 £
1
2.
–1000Y1 - 700 Y 2 - 1500 Y 3 £ 1
3.
-800 Y1 + 900 Y2 + 850 Y
3 £ 1
4.
Y1; Y2 & Y3 ³ 0
Con los coeficientes de las desigualdades de la matriz inicial:
Y1
|
Y2
|
Y3
|
C
|
-200
|
-1300
|
2000
|
1
|
-1000
|
-700
|
-1500
|
1
|
-800
|
900
|
850
|
1
|
-1
|
-1
|
-1
|
Determinar la traspuesta:
Y1
|
Y2
|
Y3
|
C
|
-200
|
-1300
|
2000
|
1
|
-1000
|
-700
|
-1500
|
1
|
-800
|
900
|
850
|
1
|
-1
|
-1
|
-1
|
Se suma una
constante para eliminar los signos negativos (en este 1500 ==> K 1500
que es el más negativo)
E.P.
Y1
|
Y2
|
Y3
|
Y4
|
Y5
|
Y6
|
C
|
|
1300
|
200
|
3500
|
1
|
0
|
0
|
1
|
(1/3500)
|
500
|
800
|
0
|
0
|
1
|
0
|
1
|
|
700
|
2400
|
2350
|
0
|
0
|
1
|
1
|
|
-1
|
-1
|
-1
|
0
|
0
|
0
|
0
|
C.P.
A. VALOR DE JUEGO = 1/ Z = 1/0.000939597 =
1064.286072 –k = - 435.71
1500
GANA
EL BANCO C (LE CUIDO SU PISTO)
B.
¿QUÉ ESTRATEGIAS VAN APLICAR C/U DE LOS COMPETIDORES?
R X1 = 0.00570469
sorteo electrodomésticos
X2 = 0
X3 = 0.00369127 sorteo de dinero en efectivo
C Y1 = 11/14900 sorteo de electrodomésticos
Y2 = 0.00201342 tasa de interés más alta
Y3 = 0
El
banco R para minimizar sus máximas
pérdidas utilizará las estrategias sortero de
electrodomésticos y sorteo de
dinero en efectivo.
El
banco C para maximizar sus máximas
ganancias utilizará la estrategia de sorteo de
electrodomésticos y la de tasa
de interés más alta.
C.
EN UN AÑO CUANTOS MESES APLICARÁ CADA ESTRATEGIA EN FUNCIÓN DE “R”.
ESTRATEGIA RESULTADOS
DEL SIMPLEX
XN = XN (VJ) Valor de Juego: Se utiliza el valor
que
resulte antes de restarle
K.
en función de “c”
Yn = Yn (VJ)
X1 = 0.0057069 (1064.286072) = 0.607142211+
X2 = 0
X3 = 0.00369127
(1064.286072)= 0.328
1.00000000
X1 = 61% Þ 7 mesas +
X2 = 0
X3 = 39% Þ 5 meses
12
meses (1 año)
Y1 = 11/14900 (1064.286072) =
0.79 Þ 9 meses
Y2 = 0.000020 (1064.286072) = 0.21 Þ 3 meses
1.0 12 meses
0.79 * 12 = 9
0.21 * 12 = 3
D.
CUANTOS CUENTAHABIENTES MÁS ATRAE
436 CUENTAHABIENTES MÁS (ES EL V.J. FINAL)












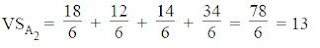






Hola, muy buena tu entrada. Podrías ayudarme con un par de ejercicios por favor.
ResponderEliminarhola , muy buenos tus ejercicios :D
ResponderEliminarhola , muy buenos tus ejercicios :D
ResponderEliminar